丸め誤差:コンピュータの落とし穴

ITを学びたい
先生、「丸め誤差」ってどういう意味ですか?よく聞くけれど、いまいち理解できていません。

IT専門家
そうですね。「丸め誤差」とは、コンピューターが計算するときに、小数点以下の数字を全部扱うことができないために起こる誤差のことです。例えば、スーパーで買い物をして、合計金額が100.5円だったとしましょう。現金で支払う場合、1円未満は切り捨てたり、四捨五入したりしますよね?コンピューターでも同じように、小数点以下の数字を処理するために、ある桁で切り捨てや四捨五入を行うため、実際の値と計算結果にわずかな違いが出てきてしまうのです。これが「丸め誤差」です。

ITを学びたい
なるほど。つまり、コンピューターは小数点以下の数字を全部は扱えないから、四捨五入みたいなことをして誤差が出てしまうということですね。ということは、この誤差をなくすことはできないのですか?

IT専門家
完全に無くすことは難しいです。でも、計算方法を工夫したり、より多くの桁数を使って計算することで、誤差を小さくすることは可能です。例えば、より細かいお金の単位を扱うようにしたり、計算の順番を変えるだけでも誤差を減らすことができます。ただ、どんな計算でも必ず誤差がゼロになるというわけではないので、プログラムを作る際には、この「丸め誤差」を考慮に入れておく必要があるのです。
丸め誤差とは。
コンピューターで計算をする際に、数字を扱う上である桁より下の細かい部分を省略することがあります。例えば、切り上げたり、切り捨てたり、四捨五入したりすることです。このような処理によって、本来の値と計算結果にわずかな違いが生じることがあります。この違いを「丸め誤差」といいます。
丸め誤差とは

計算機は、数を扱う際に、私たちが普段使っている十進数ではなく、二進数という、0と1だけの組み合わせで数を表す方法を使っています。そのため、十進数では簡単に表せる数でも、二進数ではうまく表せない場合があります。例えば、十進数の0.1は、二進数では永遠に続く数になり、完全に表すことができません。
計算機は限られた桁数しか扱えないため、この終わらない数を途中で切り捨てて処理します。この切り捨てによって生じる誤差を、丸め誤差といいます。丸め誤差は、一見すると小さな誤差ですが、計算を何度も繰り返すと、この小さな誤差が積み重なって、最終的な結果に大きな違いを生み出すことがあります。
例えば、0.1を10回足すと、本来は1になるはずです。しかし、計算機で計算すると、丸め誤差の影響で、1よりも少し大きい値や小さい値になることがあります。
この丸め誤差は、計算機を使う以上、避けることができません。特に、科学技術の計算やお金のやり取りなど、正確さが求められる場面では、この丸め誤差が大きな問題を引き起こす可能性があります。
そのため、計算機を使う際には、丸め誤差が発生することを常に意識し、誤差の影響を小さくするための工夫をする必要があります。例えば、計算の順番を変える、特別な計算方法を使うなど、様々な方法があります。これらの工夫によって、丸め誤差による問題を最小限に抑えることが重要です。
| 項目 | 説明 |
|---|---|
| 計算機の数の表現 | 二進数(0と1の組み合わせ)を使用 |
| 丸め誤差 | 二進数で正確に表現できない十進数を切り捨てることで生じる誤差 |
| 丸め誤差の影響 | 計算の繰り返しで誤差が積み重なり、最終結果に大きな違いを生む可能性 |
| 例 | 0.1を10回足すと、1にならない場合がある |
| 丸め誤差への対策 | 計算の順番を変える、特別な計算方法を使うなど |
丸め誤差の種類

数値を扱う計算において、どうしても避けられないのが丸め誤差です。これは、限られた桁数で数値を表す際に、どうしても生じてしまう小さな差のことです。丸め誤差にはいくつかの種類があり、それぞれ結果が異なってきますので、計算の目的や求められる正確さによって、適切な方法を選ぶことが重要です。
まず、切り上げについて説明します。切り上げとは、端数を常に上の位に繰り上げる方法です。例えば、1.23を小数点以下第一位で切り上げると1.3になります。1.21のように端数が小さくても、1.3に切り上げられます。つまり、常に値が大きくなる方向に調整されるのです。
次に、切り捨てについて説明します。これは切り上げとは逆に、端数を常に切り捨てる方法です。1.23を小数点以下第一位で切り捨てると1.2になります。1.29のように端数が大きくても、1.2に切り捨てられます。常に値が小さくなる方向に調整されるのが特徴です。
最後に、四捨五入について説明します。四捨五入は、端数が5以上の場合は切り上げ、4以下の場合は切り捨てる方法です。1.23は1.2になり、1.25は1.3になります。四捨五入は、切り上げと切り捨てを組み合わせた方法と言えるでしょう。
これらの方法は、それぞれ異なる結果をもたらします。例えば、銀行の利息計算のように、わずかな誤差でも大きな損失につながる可能性がある場合は、非常に高い正確さで計算を行う必要があります。そのため、状況に応じて適切な丸め方法を選択する必要があるのです。
| 丸め方法 | 説明 | 例 (1.23 を小数点以下第一位で丸める) | 値の変化 |
|---|---|---|---|
| 切り上げ | 端数を常に上の位に繰り上げる | 1.3 | 常に値が大きくなる |
| 切り捨て | 端数を常に切り捨てる | 1.2 | 常に値が小さくなる |
| 四捨五入 | 端数が5以上の場合は切り上げ、4以下の場合は切り捨て | 1.2 | 切り上げと切り捨ての組み合わせ |
丸め誤差の影響

計算を行う際に、数値を有限の桁数で表現するため、どうしても誤差が生じます。この誤差を、数値を丸めることによって生じる誤差という意味で、丸め誤差と呼びます。丸め誤差は一見小さいものですが、様々な場面で無視できない影響を及ぼすことがあります。
例えば、宇宙探査機の軌道を計算する場合を考えてみましょう。探査機の軌道は、地球や惑星の重力など、様々な要因を考慮した複雑な計算によって求められます。この計算において、わずかな丸め誤差が繰り返し発生し、蓄積されると、探査機が予定の軌道から大きく外れてしまう可能性があります。最悪の場合、探査機が目標地点に到達できなくなったり、他の天体に衝突してしまう危険性も考えられます。
また、金融システムにおいても、丸め誤差の影響は無視できません。銀行などでは、膨大な数の取引が毎日行われており、それぞれの取引においてわずかな丸め誤差が発生します。これらの誤差が積み重なると、最終的に大きな金額の損失につながる可能性があります。特に、高頻度取引のように、短時間に大量の取引を行う場合は、丸め誤差の影響がより顕著になります。
さらに、コンピュータグラフィックスの分野でも、丸め誤差は問題となります。コンピュータグラフィックスでは、画像を構成するそれぞれの点の位置や色などを数値で表現しています。これらの数値に丸め誤差が含まれると、画像に歪みやノイズが生じたり、本来滑らかに変化するはずの色が階段状に変化してしまうことがあります。このような現象は、画像の品質を低下させ、視聴者に違和感を与える可能性があります。
このように、丸め誤差は、様々な分野で軽視できない影響を与える可能性があります。そのため、丸め誤差の影響を最小限に抑えるための工夫や、丸め誤差を考慮した計算方法の開発などが重要になります。
| 分野 | 丸め誤差の影響 |
|---|---|
| 宇宙探査機の軌道計算 | わずかな丸め誤差の蓄積により、探査機が予定の軌道から大きく外れ、目標地点に到達できなくなったり、他の天体に衝突する可能性がある。 |
| 金融システム | 膨大な数の取引におけるわずかな丸め誤差の積み重ねが、最終的に大きな金額の損失につながる可能性がある。特に高頻度取引で顕著。 |
| コンピュータグラフィックス | 画像に歪みやノイズが生じたり、色の変化が階段状になるなど、画像の品質を低下させる可能性がある。 |
丸め誤差への対策

計算機で扱う数値は、限られた桁数で表現されるため、どうしても真の値との間に誤差が生じます。この誤差を丸め誤差と言い、計算を重ねるごとに蓄積し、結果に大きな影響を与えることがあります。この丸め誤差の影響を小さくするための対策をいくつかご紹介します。
まず、計算機の扱う数値の精度を上げることが有効です。例えば、単精度よりも倍精度と呼ばれる、より多くの桁数を扱える表現方法を用いることで、丸め誤差を減らすことができます。倍精度は単精度に比べて多くの桁数を扱えるため、より正確な計算を行うことが可能です。
次に、計算の順序を変えることでも丸め誤差の影響を軽減できます。例えば、たくさんの数値を足し合わせる場合、絶対値の小さな数値から順に足していくことで、誤差の蓄積を抑えることができます。これは、大きな数値に小さな数値を足しても、小さな数値の情報が丸められて失われてしまうことがあるためです。小さな数値同士を先に足し合わせることで、それらの情報の損失を最小限に抑え、より正確な結果を得ることができます。
さらに、計算方法自体を見直すことも重要です。同じ結果を求める場合でも、計算方法によって丸め誤差の影響は大きく変わります。例えば、引き算を伴う計算では、互いに近い値の引き算は結果の有効数字が大きく減少するため、なるべく引き算を避けるような計算方法を選ぶことが重要です。また、安定した計算方法として知られるアルゴリズムを採用することで、丸め誤差の影響を抑え、より信頼性の高い結果を得ることができます。
最後に、計算結果の有効数字を意識することも大切です。丸め誤差の存在により、計算結果に表示されているすべての桁が正しいとは限りません。表示されている桁数よりも少ない桁数しか信用できない場合もあります。計算の過程で発生する丸め誤差を考慮し、最終的な結果の有効数字を適切に評価することで、誤った解釈を防ぐことができます。
| 対策 | 説明 |
|---|---|
| 計算機の扱う数値の精度を上げる | 単精度よりも倍精度を用いることで、丸め誤差を減らす。 |
| 計算の順序を変える | 絶対値の小さな数値から順に足し合わせることで、誤差の蓄積を抑える。 |
| 計算方法自体を見直す | 引き算をなるべく避ける、安定したアルゴリズムを採用する。 |
| 計算結果の有効数字を意識する | 計算結果のすべての桁が正しいとは限らないことを理解し、有効数字を適切に評価する。 |
丸め誤差への理解

計算機を使う場面で、どうしても避けられないのが丸め誤差という問題です。これは、計算機が数を扱うときの仕組みが原因です。私たち人間は、無限に続く小数も分数で正確に表せますが、計算機は限られた桁数しか記憶できません。そのため、どうしても値を丸めなければならず、その過程で誤差が生じてしまいます。
丸め誤差は一見小さなものですが、計算を繰り返すと、その誤差も積み重なって大きな影響を与えることがあります。例えば、宇宙探査機の軌道計算や金融取引における高度な計算など、高い正確さが求められる場面では、丸め誤差が結果を大きく狂わせてしまう危険性があります。場合によっては、システム全体に深刻な不具合を引き起こす可能性も否定できません。
丸め誤差の影響を抑えるためには、いくつかの方法があります。例えば、計算の順序を変えることで誤差の蓄積を抑えたり、特別な計算方法を用いて誤差を小さくしたりする工夫があります。計算機の性能向上も対策の一つです。より多くの桁数を扱える計算機を使えば、丸め誤差を減らすことができます。
丸め誤差は、計算機の限界を示す重要な一面です。計算機は万能ではなく、その仕組みに inherent な限界があることを理解しておく必要があります。丸め誤差について学ぶことは、計算機を正しく理解し、より効果的に活用するために不可欠です。特に、計算を多く扱う仕事をする人にとっては、丸め誤差への理解は必須と言えるでしょう。計算結果の信頼性を確保し、思わぬ不具合を防ぐためにも、丸め誤差について深く理解し、適切な対策を心がける必要があります。
| 項目 | 内容 |
|---|---|
| 丸め誤差とは | 計算機が数を扱う際の、限られた桁数による値の丸め込みによって生じる誤差。 |
| 影響 | 計算の繰り返しにより誤差が積み重なり、大きな影響を与える可能性がある。宇宙探査機の軌道計算や金融取引など、高い正確さが求められる場面では特に危険。 |
| 対策 | 計算順序の変更、特別な計算方法の利用、計算機の性能向上(より多くの桁数を扱える計算機の使用) |
| 重要性 | 計算機の限界を示す重要な一面であり、計算機を正しく理解し、効果的に活用するために不可欠。計算を多く扱う仕事をする人にとっては必須の知識。 |
まとめ

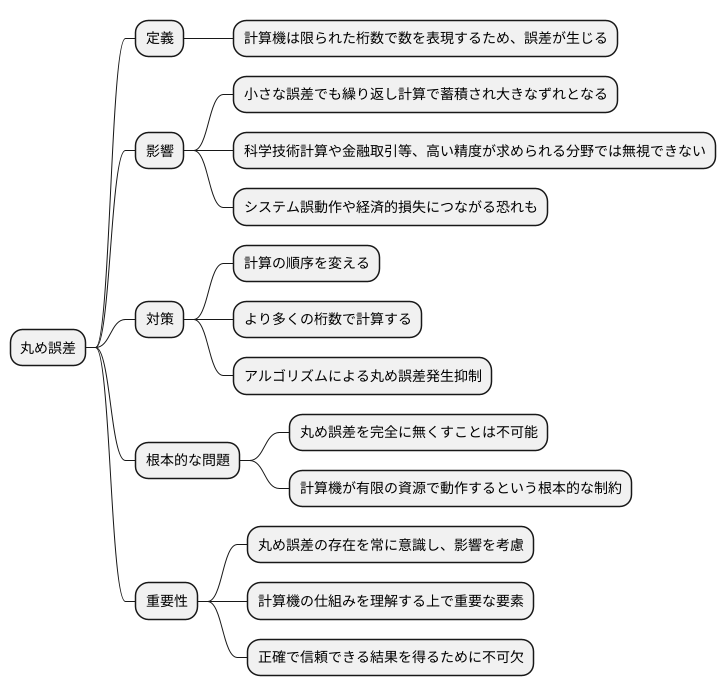
計算機は数を扱う際に、限られた桁数で表現するため、どうしても誤差が生じます。これを丸め誤差と言い、様々な場面で影響を及ぼします。例えば、少数を含む計算では、真の値と計算機の表示する値との間にわずかなずれが生じることがあります。これは、計算機が少数を有限の桁数でしか扱えないことに起因します。
丸め誤差の影響は、一見小さなものに見えますが、繰り返し計算を行うと、誤差が蓄積されて大きなずれとなる可能性があります。特に、科学技術計算や金融取引など、高い精度が求められる分野では、丸め誤差による影響を無視することはできません。場合によっては、システムの誤動作や経済的な損失につながる恐れもあります。
丸め誤差の影響を少なくするために、様々な工夫が凝らされています。例えば、計算の順序を変えることで、誤差の伝播を抑えることができます。また、より多くの桁数を使って計算することで、丸め誤差を小さくすることも可能です。計算機内部では、様々なアルゴリズムを用いて、丸め誤差の発生を抑える工夫がされています。
しかし、丸め誤差を完全に無くすことは不可能です。これは、計算機が有限の資源で動作するという根本的な制約によるものです。したがって、計算機を使う際には、丸め誤差の存在を常に意識し、その影響を考慮することが重要です。
丸め誤差への理解は、計算機の仕組みを理解する上で重要な要素です。計算機を使う上で、丸め誤差は避けて通れない問題であり、その特性を理解することは、より正確で信頼できる結果を得るために不可欠です。今後、ますます計算機が様々な分野で活用されるようになる中で、丸め誤差への理解の重要性はますます高まっていくでしょう。