遺伝的アルゴリズム:進化計算の世界

ITを学びたい
先生、「遺伝的アルゴリズム」って、生物の遺伝みたいなものをコンピューターで真似しているんですよね?でも、それがどう問題の解決につながるのか、よくわからないんです。

IT専門家
そうだね、難しいよね。たとえば、たくさんの鍵の中から、宝箱を開ける鍵を見つけたいとしよう。遺伝的アルゴリズムでは、鍵をいくつか作って、それを掛け合わせて少し違う鍵をたくさん作る。これが遺伝子の変化を真似ている部分だ。

ITを学びたい
なるほど。でも、適当に鍵を掛け合わせても、宝箱に合う鍵は見つかりにくそうですよね。

IT専門家
その通り。そこで、宝箱に合う鍵に少しでも近い鍵は残して、合わない鍵は捨てる。これを繰り返すことで、だんだん宝箱を開ける鍵に近づいていくんだ。これが自然淘汰を真似ている部分で、最適な解を見つけ出すことができるんだよ。
遺伝的アルゴリズムとは。
コンピューターのプログラムを作るうえでよく使われる『遺伝的アルゴリズム』という方法について説明します。これは、生き物の遺伝子の変化や自然淘汰の仕組みをまねて、問題の答えを導き出す方法です。別の言い方として『生成論的アルゴリズム』とも呼ばれています。
はじめに

遺伝的計算手法は、自然界における生物の進化の仕組みを模倣した、画期的な問題解決の方法です。この手法は、生物が世代交代を繰り返す中で、環境に適した遺伝子を持つ個体が生き残り、その遺伝子が次世代に受け継がれていくという自然淘汰の過程を、計算の世界で再現しています。
遺伝的計算手法では、まず、問題の解の候補を、遺伝子情報に見立てたデータで表現します。これらの解の候補は、最初の段階ではランダムに生成されます。そして、これらの解候補に対して、適応度と呼ばれる評価値を計算します。この適応度は、問題に対する解の良さ具合を表す指標であり、値が高いほど良い解であると判断されます。
次に、適応度の高い解候補を優先的に選択し、それらを基に新たな解候補を生成します。この過程は、生物の交配や突然変異といった遺伝的操作を模倣した計算処理によって行われます。交配は、複数の解候補の遺伝情報を組み合わせることで、新たな解候補を生み出す操作です。一方、突然変異は、解候補の遺伝情報の一部をランダムに変化させる操作です。これらの操作によって、多様な解候補が生成され、探索範囲が広がります。
このような選択、交配、突然変異といった操作を繰り返し行うことで、解候補の集団は徐々に進化し、より適応度の高い、つまりより良い解へと近づいていきます。従来の方法では解くのが難しい複雑な問題に対しても、遺伝的計算手法は、優れた解を見つける可能性を秘めています。そのため、近年、様々な分野で応用され、注目を集めている手法と言えるでしょう。
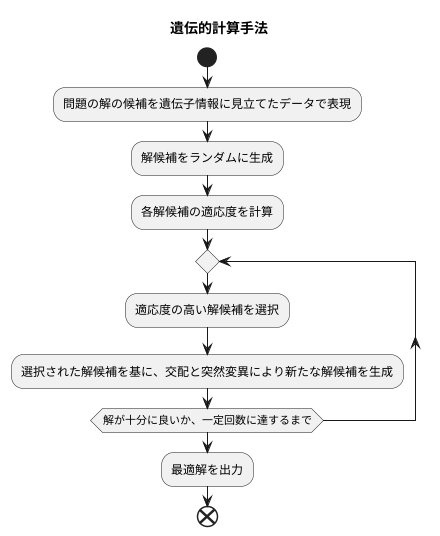
仕組み

遺伝的計算の手法は、生命の進化の仕組みを模倣した計算方法です。問題の答えを遺伝子に見立て、複数の答えの候補をまとめて集団として扱います。この集団を操作することで、より良い答えを見つけ出します。
まず、それぞれの答えの候補を遺伝子で表現します。遺伝子は、例えば0と1の並びで表されます。この遺伝子の並びが、問題に対する解の候補を表しているのです。次に、これらの解の候補を複数集めて集団を作ります。
この集団に対して、遺伝子の組み換えと変化という操作を繰り返し行います。組み換えは、二つの親の遺伝情報を組み合わせ、新しい子を作る操作です。例えば、両親の遺伝子列の前半と後半を入れ替えることで、新しい遺伝子列を持つ子が生まれます。優れた性質を持つ親から生まれた子は、親の良い性質を受け継ぎ、より良い解となる可能性が高まります。
変化は、遺伝子情報の一部をランダムに書き換える操作です。例えば、0を1に、1を0に反転させるなどです。これは、今までになかった新しい遺伝子、つまり新しい解の候補を生み出す可能性を秘めています。組み換えだけでは探索できない範囲を探索することで、思いがけない良い解が見つかるかもしれません。
これらの操作を繰り返すことで、集団全体の質が向上し、最適な答えに近づいていきます。これは、自然界の進化と同じ仕組みです。環境に適したものが生き残り、そうでないものは淘汰されていく、という自然淘汰の考え方を取り入れているのです。世代交代を繰り返す中で、より良い解を持つ個体が残り、そうでない個体は消えていきます。このようにして、遺伝的計算手法は、複雑な問題に対しても効率的に最適解を探索することができるのです。
利点

遺伝的計算手法には、様々な良い点があります。まず、とても広い範囲から答えを探す問題でも、効率的に最適な答えを見つけられるという点です。これまでの計算手法では、限られた範囲で最も良い答えを見つけることはできても、全体で見て最も良い答えを見つけるのが難しいことがありました。一部分だけを見て、その中では一番良いけれど、全体で見たらもっと良い答えがある、という状況に陥ってしまうのです。しかし、遺伝的計算手法は、まるで生物の集団のようにたくさんの答えを同時に考えます。そのため、様々な可能性を比較検討し、限られた範囲だけで満足することなく、全体で見て最も良い答えに近い答えを見つけ出す可能性が高まります。
また、問題の詳しい仕組みを知らなくても使えるという点も大きな利点です。例えば、果物の甘さを競うコンテストで、一番甘い果物を見つけることを想像してみてください。遺伝的計算手法では、果物の甘さを数値で表す方法さえ分かれば、果物がどのように甘くなるのかという詳しい仕組みを知らなくても、一番甘い果物を見つけ出すことができます。問題を遺伝子という形で表現し、それぞれの遺伝子の良さを評価する仕組みを作れば、様々な分野の問題に適用できるのです。
この手法は、複雑な計算を必要とする様々な場面で力を発揮します。例えば、工場で製品を作る手順を最適化したり、配送ルートを効率化したり、新しい材料の組み合わせを見つけ出したりといった用途が考えられます。従来の方法では難しかった問題に対しても、遺伝的計算手法は画期的な解決策を提供してくれる可能性を秘めているのです。
| メリット | 説明 |
|---|---|
| 効率的な最適解の探索 | 広範囲から全体で見て最も良い答えに近い答えを見つけられる。限られた範囲での最適解ではなく、全体最適に近い解を探索可能。 |
| 問題の仕組みに関する知識不要 | 問題の詳しい仕組みを知らなくても、評価基準さえあれば最適解を探索可能。様々な分野への適用が可能。 |
| 複雑な問題への適用 | 工場の工程最適化、配送ルート効率化、新素材開発など、複雑な計算が必要な場面で有効。従来手法では困難な問題への解決策となる可能性。 |
応用例

遺伝的仕組みをまねた計算手法である遺伝的アルゴリズムは、様々な分野で活用されています。
まず、機械学習の分野では、人工知能の学習方法をより良くするために役立っています。例えば、人間の脳の神経回路網を模倣した数理モデルであるニューラルネットワークの構造を最適化したり、学習の効率を上げるための最適な調整値を見つけ出したりする際に利用されます。これにより、より精度の高い人工知能を開発することが可能になります。
また、製造業においても、遺伝的アルゴリズムは生産効率の向上に貢献しています。工場全体の作業手順を効率的に計画したり、製造ロボットの動きを細かく調整したりすることで、無駄を省き、生産性を高めることができます。
金融の分野では、資産運用の効率化に役立っています。複数の金融商品を組み合わせた運用方法を最適化したり、将来の株価の動きを予測したりすることで、投資による利益を最大化することが期待できます。
さらに、娯楽産業であるゲーム開発においても、ゲームの面白さを高めるために利用されています。ゲームに登場するキャラクターの行動を制御する人工知能を開発する際に、遺伝的アルゴリズムを用いることで、より人間らしい、あるいはより賢いキャラクターを生み出すことができます。このように、遺伝的アルゴリズムは様々な産業で革新をもたらす可能性を秘めた技術と言えるでしょう。
| 分野 | 活用例 | 効果 |
|---|---|---|
| 機械学習 | ニューラルネットワークの構造最適化、学習効率向上のための調整値探索 | より精度の高い人工知能の開発 |
| 製造業 | 工場の作業手順計画、製造ロボットの動作調整 | 生産効率の向上 |
| 金融 | 資産運用の最適化、株価予測 | 資産運用の効率化 |
| ゲーム開発 | ゲームキャラクターのAI開発 | ゲームの面白さの向上 |
課題

遺伝的アルゴリズムは、生物の進化に着想を得た強力な問題解決手法です。しかし、その優れた可能性の一方で、いくつかの乗り越えるべき課題も抱えています。
まず、計算時間の長さが挙げられます。遺伝的アルゴリズムは、多数の解候補を生成し、それらを繰り返し組み合わせてより良い解を探索していくため、問題の規模が大きくなると、計算に膨大な時間を要する場合があります。特に、解候補の評価に時間のかかる複雑な問題では、この計算時間の増大が深刻な制約となることがあります。
次に、適切な設定値を見つけることの難しさが課題となります。遺伝的アルゴリズムには、突然変異の確率や交叉の方法など、様々な設定値が存在します。これらの設定値は、問題の性質や規模によって最適な値が異なり、適切な設定値を見つけるためには、試行錯誤を繰り返す必要が生じることがあります。最適な設定値の探索は、熟練した経験と知識を必要とする複雑な作業であり、遺伝的アルゴリズムの利用を困難にする一因となっています。
さらに、全ての状況において万能ではないという点も忘れてはなりません。遺伝的アルゴリズムは、様々な問題に適用できる汎用的な手法ですが、問題によっては他の手法の方が効率的に解を導き出せる場合があります。例えば、解空間が滑らかで連続的な問題では、勾配法などの最適化手法の方が適していると考えられます。問題の性質を見極め、適切な手法を選択することが重要です。
これらの課題を克服するために、様々な研究が行われています。並列計算技術を用いて計算時間を短縮する研究や、機械学習を用いて自動的に最適な設定値を探索する研究などが盛んに行われています。このような研究の進展によって、遺伝的アルゴリズムは今後さらに発展し、より幅広い問題への適用が期待されています。進化計算という大きな枠組みの中で、遺伝的アルゴリズムは、より複雑で困難な問題の解決に貢献していくものと確信しています。
| 課題 | 詳細 |
|---|---|
| 計算時間の長さ | 多数の解候補の生成と反復的な組み合わせ探索により、問題の規模が大きくなると計算時間が膨大になる。特に、解候補の評価に時間のかかる複雑な問題では深刻な制約となる。 |
| 適切な設定値を見つけることの難しさ | 突然変異の確率や交叉の方法など、様々な設定値が存在し、問題の性質や規模によって最適な値が異なる。適切な設定値を見つけるには試行錯誤が必要で、熟練した経験と知識を要する。 |
| 全ての状況において万能ではない | 汎用的な手法だが、問題によっては他の手法の方が効率的。例えば、解空間が滑らかで連続的な問題では勾配法などが適している。問題の性質を見極め、適切な手法を選択することが重要。 |
まとめ

遺伝的アルゴリズムは、自然淘汰や突然変異といった生物の進化に見られる仕組みを、計算の手法に取り入れた、強力な最適化手法です。この手法は、様々な問題に対して、最適な解を効率的に探し出すことができます。まるで生物が環境に適応するように、与えられた条件のもとで最も良い答えを見つけ出すのです。
遺伝的アルゴリズムが特に有効なのは、複雑で従来の方法では解きにくい問題です。例えば、様々な制約条件がある中での資源配分や、複雑な形状の最適設計など、多くの要素が絡み合い、最適解を見つけるのが難しい問題に対して、優れた効果を発揮します。試行錯誤を繰り返す中で、徐々に良い解へと近づいていくという、生物の進化に似たプロセスを経て、最適解を探索していくのです。
遺伝的アルゴリズムは、様々な分野で応用されています。例えば、工場の生産計画や、物流における配送ルートの最適化、さらには金融商品のポートフォリオ設計など、幅広い分野で活用されています。また、機械学習の分野でも、最適なモデルのパラメータを探索するために利用されるなど、その応用範囲はますます広がっています。
一方で、遺伝的アルゴリズムには、いくつかの課題も存在します。計算に時間がかかる場合があることや、アルゴリズムのパラメータ設定が難しく、適切な設定を見つけるのに試行錯誤が必要となる場合があることなどです。しかし、これらの課題に対して、多くの研究者が活発に研究に取り組んでおり、アルゴリズムの改良や高速化、パラメータ自動調整技術の開発などが進められています。
遺伝的アルゴリズムは、進化計算と呼ばれる計算手法の中でも中心的な役割を担っており、今後の発展が大きく期待されています。生物の進化という自然の摂理から着想を得たこのアルゴリズムは、まさに計算機科学における革新と言えるでしょう。今後、更なる研究開発によって、より広範な問題解決に貢献していくことが期待されます。
| 項目 | 内容 |
|---|---|
| 概要 | 生物の進化(自然淘汰、突然変異)を模倣した最適化手法 |
| 利点 | 複雑な問題の最適解を効率的に探索可能 |
| 有効な問題 | 従来の方法では解きにくい、複雑で多くの要素が絡み合う問題(例: 資源配分、形状の最適設計) |
| 探索プロセス | 試行錯誤を繰り返し、徐々に良い解へ近づく(生物の進化に類似) |
| 応用分野 | 工場の生産計画、物流における配送ルートの最適化、金融商品のポートフォリオ設計、機械学習におけるモデルのパラメータ探索など |
| 課題 | 計算時間、パラメータ設定の難しさ |
| 課題への取り組み | アルゴリズムの改良、高速化、パラメータ自動調整技術の開発 |
| 将来展望 | 進化計算の中心的役割、更なる研究開発による広範な問題解決への貢献 |
